Предмет: Алгебра (для 9-11 классов).
Педагог: Елена Викторовна Кирина – учитель математики МАОУ «Центр образования №13 им. Н.А. Кузнецова».
Тема: Задачи на проценты.
ПРОЦЕНТЫ
«Не делай никогда того, чего не знаешь, но научись всему, что следует знать». (Пифагор)
Историческая справка. Слово «процент» происходит от латинского слова pro centum,что буквально означает «за сотню» или «со ста». Процентами очень удобно пользоваться на практике, так как они выражают части целых чисел в одних и тех же сотовых долях. Процент - это частный вид десятичных дробей, сотая доля целого. Знак «%» происходит, как полагают, от итальянского слова cento (сто), которое в процентных расчетах часто писалось сокращенно cto. Отсюда путем дальнейшего упрощения в скорописи буквы t в наклонную черту произошел современный символ для обозначения процента. Существует и другая версия возникновения этого знака. Предполагается, что этот знак произошел в результате нелепой опечатки, совершенной наборщиком. В 1685 году в Париже была опубликована книга – руководство по коммерческой арифметике, где по ошибке наборщик вместо cto напечатал %. Задачи на проценты, как правило, описывают жизненную ситуацию. В ней присутствует какая-то величина, которая увеличивается или уменьшается на сколько-то процентов. Таким образом, в задаче на проценты упоминается такие данные, как первоначальная величина, конечная величина и процент, на который эта величина изменилась. Чаще всего в задаче требуется найти либо первоначальную величину, либо конечную величину, реже – процент, на который эта величина изменилась. Задачи с процентами часто попадаются в экзаменационных заданиях. Многих они сбивают с толку – как разобраться с условием и как это решить? И совершенно зря, потому что с задачами на проценты каждый часто встречается в обычной жизни. Чтобы стало понятнее, мы сейчас рассмотрим примеры из обычной жизни, где вам могут встретиться проценты. И все у вас станет на свои места. Итак, мы помним, что один процент – это одна сотая доля числа. При решении задачи на проценты первым делом нужно определить вид задачи. Типы задач на проценты Тип 1: Находим процент от числа.- Задача.За месяц на предприятии изготовили 500 приборов. 20% изготовленных приборов не смогли пройти контроль качества. Сколько приборов не прошло контроль качества?
- Решение.Нужно найти 20% от общего количества изготовленных приборов. 20% = 0,2 . 500 * 0,2 = 100. 100 из общего количества изготовленных приборов контроль не прошло.
- Задача.Готовясь к экзамену, школьник решил 38 задач из пособия для самоподготовки. Что составляет 23% числа всех задач в пособии. Сколько всего задач собрано в этом пособии для самоподготовки?
- Решение.Мы не знаем, сколько всего задача в пособии. Но зато нам известно, что 38 задач составляют 25% от общего их количества. Запишем 23% в виде дроби: 0,23. Далее нам следует известную нам часть целого разделить на ту долю, которую она составляет от всего целого: 38:0,25 = 152. Именно 152 задачи включили в этот сборник.
- Задача.В классе 30 учеников. 14 из них – девочки. Сколько процентов девочек в классе?
- Решение.Чтобы узнать, какой процент составляет одно число от другого, нужно то число, которое требуется найти, разделить на общее количество и умножить на 100%. Значит, 14:30*100% = 47%.
- Задача.На прошлогоднем экзамене по математике 140 старшеклассников получили пятерки. В этом году число отличников выросло на 15%. Сколько человек получили пятерки за экзамен по математике в этом году?
- Решение. Если некое число а увеличено на х%, то оно увеличилось в (1 + х /100) раз. Откуда а * (1 + х /100). Подставим в эту формулу данные нам по условию задачи цифры и получим ответ: 140 * (1 + 15/100) = 161.
- Задача.Год назад школу закончили 100 ребят. А в это году выпускников на 25 меньше. Сколько выпускников в этом году?
- Решение.Если число а уменьшено на х% и при этом 0 ≤ х ≤ 100, то число уменьшено в (1 – х/100) раз. И нужное нам число находим по формуле а * (1 – х/100). Подставляем цифры из условия задачи и получаем ответ: 100 * (1 – 25/100) = 75.
- Задача.Родители взяли в банке кредит 5000 рублей сроком на год под 15% ежемесячно. Сколько денег они заплатят банку через год?
- Решение.Простые проценты называются так, потому что они начисляются многократно, но всякий раз к исходной сумме. Если обозначить исходную сумму как а, сумму, которая наращивается, как S, процентную ставку как х% и количество периодов начисления процента как у, то формулу можно записать так: S = а * (1 + у * х/100). Теперь подставим сюда цифры из условия задачи и узнаем, сколько денег родители заплатят банку: S = 5000 * (1 + 12 * 15/100) = 14000.
- Задача.На этот раз сумма кредита 25000 рублей, взятых под те же 15% сроком на 3 месяца. Снова надо узнать, сколько денег придется заплатить банку по истечении срока кредита.
- Решение. Сложные проценты отличаются от простых тем, что процент много раз начисляется не к исходной сумме, а к сумме с уже начисленными раньше процентами. Пускай снова S – наращиваемая сумма, а– исходная, х% - процентная ставка, у – количество периодов начисления процента. В этом случае формула принимает вид: S = а * (1 + х/100)у. Подставляем цифры из условия: S = 25000 * (1 + 15/100)3 = 38021,875 – искомая сумма.
- Задание. В городе проживало 30 000 человек. В результате строительства нового микрорайона количество жителей увеличилось на 6%. Сколько человек стало проживать в городе?
- Задание Сберегательный банк начисляет на срочный вклад 20% годовых. Вкладчик положил на счет 800 р. Какая сумма будет на этом счете через год, если никаких операций со счетом проводиться не будет?
- Задание Товар на распродаже уценили на 20%, при этом он стал стоить 680 р. Сколько стоил товар до распродажи?
- Задание На предприятии работало 240 сотрудников. После модернизации производства их число сократилось до 192. На сколько процентов сократилось число сотрудников предприятия?
- Найдём число сокращённых людей: 240 - 192 = 48 (чел); 3. Найдём процент сокращённых: 48 : 240 ∙ 100 % = 20 %; Ответ: при модернизации производства было сокращено 20 % рабочих.
- Задание В начале учебного года в школе было 1250 учащихся, а к концу года их стало 950. На сколько процентов уменьшилось за год число учащихся?
- В задачах на проценты – переходим от процентов к конкретным величинам. Или, если надо – от конкретных величин к процентам.Внимательно читаем задачу!
- Очень тщательно изучаем,от чего нужно считать проценты. Если об этом не сказано прямым текстом, то обязательно подразумевается. При последовательном изменении величины, проценты подразумеваются от последнего значения. Внимательно читаем задачу!
- Закончив решать задачу, читаем её ещё раз. Вполне возможно, вы нашли промежуточный ответ, а не окончательный.Внимательно читаем задачу!
- Средний вес мальчиков того же возраста, что и Сергей, равен 48 кг. Вес Сергея составляет 120% среднего веса. Сколько весит Сергей? (57, 6)
- В начале года число абонентов телефонной компании «Север» составляло 200 тыс. чел., а в конце года их стало 210 тыс. чел. На сколько процентов увеличилось за год число абонентов этой компании? (5)
- На счет в банке, доход по которому составляет 15% годовых, внесли 24 тыс. р. Сколько тысяч рублей будет на этом счете через год, если никаких операций со счетом проводиться не будет? (27,6)
- Какая сумма (в рублях) будет проставлена в кассовом чеке, если стоимость товара 520 р., и покупатель оплачивает его по дисконтной карте с 5%-ной скидкой? (494)
- В понедельник некоторый товар поступил в продажу по цене 1000 р. В соответствии с принятыми в магазине правилами цена товара в течение недели остается неизменной, а в первый день каждой следующей недели снижается на 20% от предыдущей цены. Сколько рублей будет стоить товар на двенадцатый день после поступления в продажу? (800).
Предмет: Химия (для 9-11 классов).
Педагог: кандидат химических наук Оксана Геннадьевна Четырина.
Тема: Щелочные и щелочноземельные металлы и их соединения.
Щелочные и щелочноземельные металлы и их соединения Общие свойства металлов Главную подгруппу I группы Периодической системы Д.И. Менделеева составляют литий Li, натрий Na, калий K, рубидий Rb, цезий Cs и франций Fr. Элементы этой подгруппы относят к щелочным металлам. Щелочноземельные металлы находятся в главной подгруппе II группы Периодической системы Д.И. Менделеева. Это кальций Ca, стронций Sr, барий Ba и радий Ra. Щелочные и щелочноземельные металлы как типичные металлы проявляют ярко выраженные восстановительные свойства. У элементов главных подгрупп металлические свойства с увеличением радиуса возрастают. Особенно сильно восстановительные свойства проявляются у щелочных металлов. Настолько сильно, что практически невозможно проводить их реакции с разбавленными водными растворами, так как в первую очередь будет идти реакция взаимодействия их с водой. У щелочноземельных металлов ситуация аналогичная. Они тоже взаимодействуют с водой, но гораздо менее интенсивно, чем щелочные металлы. Электронные конфигурации валентного слоя щелочных металлов – ns1, где n – номер электронного слоя. Их относят к s-элементам. У щелочноземельных металлов – ns2 (s-элементы). Эти элементы образуют соединения с ионным типом связи. При образовании соединений для них степень окисления соответствует номеру группы. Обнаружение ионов металла в солях Ионы металлов легко определить по изменению окраски пламени: соли лития – карминово-красная окраска пламени, соли натрия – желтая, соли калия – фиолетовый через кобальтовое стекло, рубидия – красная, цезия – голубовато-синяя, стронция – карминово-красная и бария – жёлто-зелёная.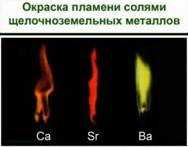
 Соли щелочных и щелочноземельных металлов используются для создания фейерверков. И можно легко определить по окраске, соли какого металла применялись.
Свойства щелочных металлов
Физические свойства
Щелочные металлы – это серебристо-белые вещества с характерным металлическим блеском. Они быстро тускнеют на воздухе из-за окисления. Это мягкие металлы, по мягкости Na, K, Rb, Cs подобны воску. Они легко режутся ножом. Они легкие. Литий – самый легкий металл с плотностью 0,5 г/см3.
Химические свойства
Соли щелочных и щелочноземельных металлов используются для создания фейерверков. И можно легко определить по окраске, соли какого металла применялись.
Свойства щелочных металлов
Физические свойства
Щелочные металлы – это серебристо-белые вещества с характерным металлическим блеском. Они быстро тускнеют на воздухе из-за окисления. Это мягкие металлы, по мягкости Na, K, Rb, Cs подобны воску. Они легко режутся ножом. Они легкие. Литий – самый легкий металл с плотностью 0,5 г/см3.
Химические свойства
- Взаимодействие с неметаллами
- Взаимодействие с кислородом
- Взаимодействие с водой
- Взаимодействие с кислотами – сильными окислителями
| Распространенные соединения щелочных металлов | |
| NaOH | Едкий натр (каустическая сода) |
| NaCl | Поваренная соль |
| NaNO3 | Чилийская селитра |
| Na2SO4∙10H2O | Глауберова соль |
| Na2CO3∙10H2O | Сода кристаллическая |
| KOH | Едкое кали |
| KCl | Хлорид калия (сильвин) |
| KNO3 | Индийская селитра |
| K2CO3 | Поташ |
- Взаимодействие с неметаллами
- Взаимодействие с кислородом
- Взаимодействие с водой
- Взаимодействие с кислотами – сильными окислителями
 СaO + H2O → Ca(OH)2
Ca(OH)2 + CO2↑ → CaCO3↓+ H2O
CaCO3↓+ H2O + CO2 → Ca(HCO3)2
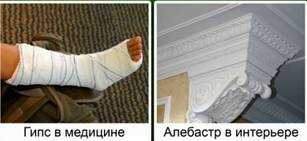
Гипс – это CaSO4∙2H2O, алебастр – CaSO4∙0,5H2O. Гипс и алебастр используются в строительстве, в медицине и для изготовления декоративных изделий.
Карбонат кальция CaCO3 образует множество различных минералов.
СaO + H2O → Ca(OH)2
Ca(OH)2 + CO2↑ → CaCO3↓+ H2O
CaCO3↓+ H2O + CO2 → Ca(HCO3)2
Гипс – это CaSO4∙2H2O, алебастр – CaSO4∙0,5H2O. Гипс и алебастр используются в строительстве, в медицине и для изготовления декоративных изделий.
Карбонат кальция CaCO3 образует множество различных минералов.
 Фосфат кальция Ca3(PO4)2 – фосфорит, фосфорная мука используется как минеральное удобрение.
Чистый безводный хлорид кальция CaCl2 – это гигроскопичное вещество, поэтому широко применяется в лабораториях как осушитель.
Карбид кальция – CaC2. Его можно получить так:
СaO + 2C →CaC2 +CO.
Одно из его применений – это получение ацетилена.
CaC2 + 2H2O →Ca(OH)2 + C2H2↑
Сульфат бария BaSO4 – барит. Используется как эталон белого в некоторых исследованиях.
Фосфат кальция Ca3(PO4)2 – фосфорит, фосфорная мука используется как минеральное удобрение.
Чистый безводный хлорид кальция CaCl2 – это гигроскопичное вещество, поэтому широко применяется в лабораториях как осушитель.
Карбид кальция – CaC2. Его можно получить так:
СaO + 2C →CaC2 +CO.
Одно из его применений – это получение ацетилена.
CaC2 + 2H2O →Ca(OH)2 + C2H2↑
Сульфат бария BaSO4 – барит. Используется как эталон белого в некоторых исследованиях.
 Жесткость воды
В природной воде содержатся соли кальция и магния. Если они содержатся в заметных концентрациях, то в такой воде не мылится мыло из-за образования нерастворимых стеаратов. При её кипячении образуется накипь.
Временная жесткость обусловлена присутствием гидрокарбонатов кальция и магния Ca(HCO3)2 и Mg(HCO3)2. Такую жесткость воды можно устранить кипячением
Ca(HCO3)2 CaCO3↓ + СО2↑ + Н2О
Постоянная жесткость воды обусловлена наличием катионов Ca2+, Mg2+ и анионов H2PO4-, Cl-, NO3- и др. Постоянная жесткость воды устраняется только благодаря реакциям ионного обмена, в результате которых ионы магния и кальция будут переведены в осадок
CaCl2 + Na2CO3 → CaCO3↓ + 2NaCl.
Жесткость воды
В природной воде содержатся соли кальция и магния. Если они содержатся в заметных концентрациях, то в такой воде не мылится мыло из-за образования нерастворимых стеаратов. При её кипячении образуется накипь.
Временная жесткость обусловлена присутствием гидрокарбонатов кальция и магния Ca(HCO3)2 и Mg(HCO3)2. Такую жесткость воды можно устранить кипячением
Ca(HCO3)2 CaCO3↓ + СО2↑ + Н2О
Постоянная жесткость воды обусловлена наличием катионов Ca2+, Mg2+ и анионов H2PO4-, Cl-, NO3- и др. Постоянная жесткость воды устраняется только благодаря реакциям ионного обмена, в результате которых ионы магния и кальция будут переведены в осадок
CaCl2 + Na2CO3 → CaCO3↓ + 2NaCl. 
