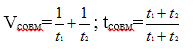Алгебра – текстовые задачи в билета ЕГЭ
Для учителей математики не секрет, что решение текстовых задач вызывает у учащихся трудности, в каком бы возрасте они не находились. Трудности связаны элементарно с прочтения текста задачи. У значительного процента школьников средней школы не сформировано умение читать и понимать текст одновременно. Понятно, что дефицит такого качества чтения делает весьма затруднительным выбор структурированной информации и поиск нужной стратегии при решении, сформулированной в виде сюжетного смыслового текста учебной задачи. Помогут разобраться в этом наши гости вместе с ведущим цикла журналистом Константином Денисовым. Текстовые задачи входят в содержание единого экзамена в 9 класса и 11 класса. При этом большинство учащихся 11 классов не в полной мере владеют техникой решения текстовых задач и не умеют за их часто нетрадиционной формулировкой увидеть типовые задания, которые были достаточно хорошо отработаны на уроках в рамках школьной программы. Решение задач занимает в математическом образовании огромное место. Умение решать задачи, является одним из основных показателей уровня математического развития, глубины освоения учебного материала. Текстовые задачи – традиционно трудный материал для значительной части школьников. Во многом это связано с необходимостью четкого осознания различных соотношений между описываемыми в тексте задачи объектами. Умение решать ту или иную задачу зависит от многих факторов. Однако прежде всего необходимо научиться различать основные типы задач и уметь решать простейшие из них. Рассмотрим типовые задачи и их решения, а именно: - задачи на движение; - задачи на производительность; - задачи на сплавы и смеси. Задачи на движение. При решении задач на движение принимают следующие допущения: - движение считается равномерным, если нет специальных оговорок; - изменение направления движения и переходы на новый режим движения считаются происходящими мгновенно; - скорость считается числом положительным; - если тело движется по течению реки, то его скорость слагается из скорости в стоячей воде и скорости течения реки, если против течения реки, то скорость равна разности скорости в стоячей воде и скорости течения реки; - если два тела начинают движение одновременно (при этом движутся они в одном направлении), то в случае, если они встречаются, каждое тело с момента выхода и до встречи затрачивает одинаковое время. Основные формулы, используемые при решении задач на движение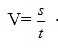 - скорость движущегося объекта прямо пропорциональна пути S и обратно пропорциональна времени t;
- скорость движущегося объекта прямо пропорциональна пути S и обратно пропорциональна времени t;
| Скорость V | Время t | Расстояние S | |
| 1 объект | |||
| 2 объект |
 Задача 2. Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми равно 70 км. На следующий день он отправился обратно в A со скоростью на 3 км/ч больше прежней. По дороге он сделал остановку на 3 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость велосипедиста на пути из B в A. Ответ дайте в км/ч.
Решение:
Задача 2. Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми равно 70 км. На следующий день он отправился обратно в A со скоростью на 3 км/ч больше прежней. По дороге он сделал остановку на 3 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость велосипедиста на пути из B в A. Ответ дайте в км/ч.
Решение:
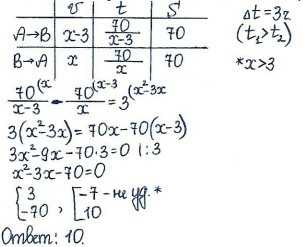 Задача 3. Из двух городов, расстояние между которыми равно 560 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч?
Решение:
Задача 3. Из двух городов, расстояние между которыми равно 560 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч?
Решение:
 Задача 4. Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 8 км. Путь из А в В занял у туриста 5 часов, из которых 1 час ушёл на спуск. Найдите скорость туриста на спуске, если она больше скорости на подъёме на 3 км/ч. Ответ дайте в км/ч.
Решение:
Задача 4. Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 8 км. Путь из А в В занял у туриста 5 часов, из которых 1 час ушёл на спуск. Найдите скорость туриста на спуске, если она больше скорости на подъёме на 3 км/ч. Ответ дайте в км/ч.
Решение:
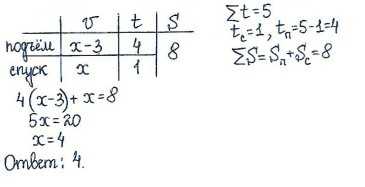 Задача 5. Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 300 метрам?
Решение:
Задача 5. Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 300 метрам?
Решение:
 Задачи на движение по воде.
В задачах на движение по воде необходимо помнить формулы:
Vпо теч = Vсоб+Vтеч
Vпротив теч = Vсоб-Vтеч
Задачи на движение по воде.
В задачах на движение по воде необходимо помнить формулы:
Vпо теч = Vсоб+Vтеч
Vпротив теч = Vсоб-Vтеч
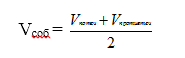 Скорость плота считается равной скорости реки.
Задача 1. Теплоход, скорость которого в неподвижной воде равна 25 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 3 км/ч, стоянка длится 5 часов, а в исходный пункт теплоход возвращается через 30 часов после отплытия из него. Сколько километров прошёл теплоход за весь рейс?
Решение:
Скорость плота считается равной скорости реки.
Задача 1. Теплоход, скорость которого в неподвижной воде равна 25 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 3 км/ч, стоянка длится 5 часов, а в исходный пункт теплоход возвращается через 30 часов после отплытия из него. Сколько километров прошёл теплоход за весь рейс?
Решение:
 Задача 2. Баржа проплыла по течению реки 60 км и, повернув обратно, проплыла ещё 20 км, затратив на весь путь 7 часов. Найдите собственную скорость баржи, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.
Решение:
Задача 2. Баржа проплыла по течению реки 60 км и, повернув обратно, проплыла ещё 20 км, затратив на весь путь 7 часов. Найдите собственную скорость баржи, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.
Решение:
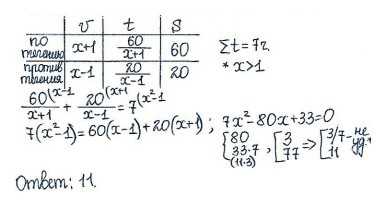 Задача 3. От пристани А к пристани В, расстояние между которыми равно 130 км, отправился с постоянной скоростью первый теплоход, а через 3 часа после этого следом за ним со скоростью на 3 км/ч большей отправился второй. Найдите скорость второго теплохода, если в пункт В он прибыл одновременно с первым. Ответ дайте в км/ч.
Решение:
Задача 3. От пристани А к пристани В, расстояние между которыми равно 130 км, отправился с постоянной скоростью первый теплоход, а через 3 часа после этого следом за ним со скоростью на 3 км/ч большей отправился второй. Найдите скорость второго теплохода, если в пункт В он прибыл одновременно с первым. Ответ дайте в км/ч.
Решение:
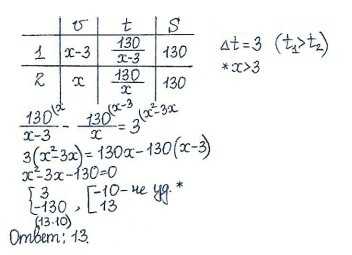 Задачи на движение по окружности.
Движение по замкнутой трассе (допустим по стадиону) похоже на движение вдогонку если 2 бегуна начинают двигаться по окружности одновременно с разными скоростями собственно V1 и V2 (V1>V2), то 1 бегун приближается ко 2 со скоростью V1-V2 и в момент, когда 1 бегун догоняет 2 бегуна, то 1 бегун как раз проходит на один круг больше второго и поэтому время считается так:
Задачи на движение по окружности.
Движение по замкнутой трассе (допустим по стадиону) похоже на движение вдогонку если 2 бегуна начинают двигаться по окружности одновременно с разными скоростями собственно V1 и V2 (V1>V2), то 1 бегун приближается ко 2 со скоростью V1-V2 и в момент, когда 1 бегун догоняет 2 бегуна, то 1 бегун как раз проходит на один круг больше второго и поэтому время считается так: 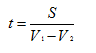 Задача 1. Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение:
Задача 1. Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение:
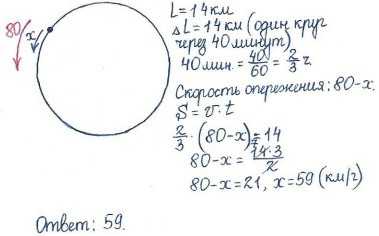 Задача 2. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
Решение:
Задача 2. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
Решение:
 Задачи на определение средней скорости.
Если S-путь, пройденный телом, а t-время, за которое этот путь пройден, то средняя скорость вычисляется по формуле:
Задачи на определение средней скорости.
Если S-путь, пройденный телом, а t-время, за которое этот путь пройден, то средняя скорость вычисляется по формуле: 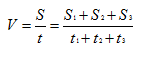 Задача. Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час – со скоростью 100 км/ч, а затем два часа – со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
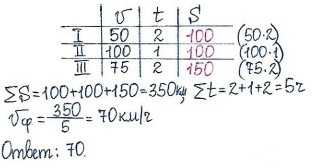
Задача. Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час – со скоростью 100 км/ч, а затем два часа – со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
 Задачи на движение протяженных тел.
В задачах на движение протяженных тел требуется определить длину одного из них наиболее типичные ситуации: определение длины поезда, проезжающего мимо:
Задачи на движение протяженных тел.
В задачах на движение протяженных тел требуется определить длину одного из них наиболее типичные ситуации: определение длины поезда, проезжающего мимо:
- придорожного столба
- идущего параллельно путем пешехода
- лесополосы определенной длины
- другого двигающего поезда
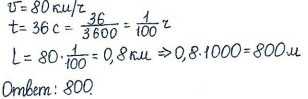 Задача 2. Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 400 метрам, за 1 минуту. Найдите длину поезда в метрах.
Решение:
Задача 2. Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 400 метрам, за 1 минуту. Найдите длину поезда в метрах.
Решение:
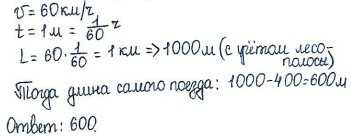 Задачи на производительность
Задачи на выполнение определенного объема работы по своему решению очень схожи с задачами на движение: объем работы выполняет роль расстояния, а производительность выполняет роль скорости. В тех случаях, когда объем работы не задан, его принимают за 1.
При решении задач, связанных с выполнением определенного объема работы, используют следующие соотношения:
Задачи на производительность
Задачи на выполнение определенного объема работы по своему решению очень схожи с задачами на движение: объем работы выполняет роль расстояния, а производительность выполняет роль скорости. В тех случаях, когда объем работы не задан, его принимают за 1.
При решении задач, связанных с выполнением определенного объема работы, используют следующие соотношения:
- A=p*t, где А- количество работы, t-время выполнения работы, p-производительность труда, т.е количество работы, выполняемой в единицу времени.
- Если весь объем работы, принятый за единицу, выполняется одним работником за t1, а вторым за t2, то производительность труда при их совместной работе

 Задача 2. Игорь и Паша красят забор за 9 часов, Паша и Володя – за 12 часов, а Володя и Игорь – за 18 часов. За сколько часов мальчики покрасят забор, работая втроём?
Решение:
Задача 2. Игорь и Паша красят забор за 9 часов, Паша и Володя – за 12 часов, а Володя и Игорь – за 18 часов. За сколько часов мальчики покрасят забор, работая втроём?
Решение:
 Задача 3. Саша отвечает за 1 час на 8 вопросов теста, а Денис – на 9. Они одновременно начали отвечать на вопросы теста, и Саша закончил позже Дениса на 10 минут. Сколько вопросов содержит тест?
Решение:
Задача 3. Саша отвечает за 1 час на 8 вопросов теста, а Денис – на 9. Они одновременно начали отвечать на вопросы теста, и Саша закончил позже Дениса на 10 минут. Сколько вопросов содержит тест?
Решение:
 Задачи на сплавы и смеси.
Задачи на смеси и сплавы встречаются не только в математике, но и в химии, где рассматриваются различные соединения. Они вызывают затруднения у школьников, в частности, у выпускников. Очень важно разобраться в самом тексте задачи. Необходимо научиться расчленять такую задачу на ряд простейших.
В таких задачах используются понятия «концентрация», «процентное содержание», «влажность».
Если смесь (сплав, раствор) имеет массу m, и состоит из вещества массой m1, то величина
Задачи на сплавы и смеси.
Задачи на смеси и сплавы встречаются не только в математике, но и в химии, где рассматриваются различные соединения. Они вызывают затруднения у школьников, в частности, у выпускников. Очень важно разобраться в самом тексте задачи. Необходимо научиться расчленять такую задачу на ряд простейших.
В таких задачах используются понятия «концентрация», «процентное содержание», «влажность».
Если смесь (сплав, раствор) имеет массу m, и состоит из вещества массой m1, то величина 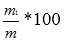 называются процентным содержанием вещества.
Задача 1. Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 18-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение:
называются процентным содержанием вещества.
Задача 1. Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 18-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение:
 Задача 2. Смешали 4 литра 15-процентного водного раствора некоторого вещества с 6 литрами 25-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение:
Задача 2. Смешали 4 литра 15-процентного водного раствора некоторого вещества с 6 литрами 25-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение:
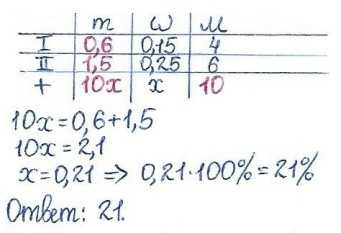 Задача 3. Первый сплав содержит 10% меди, второй – 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Решение:
Задача 3. Первый сплав содержит 10% меди, второй – 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Решение:
 Задача 4. Имеются два сосуда с растворами кислоты различной концентрации. Первый содержит 30 кг раствора, а второй – 20 кг раствора. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Решение:
Задача 4. Имеются два сосуда с растворами кислоты различной концентрации. Первый содержит 30 кг раствора, а второй – 20 кг раствора. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Решение:
 Задача 5. Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси.
Решение:
Задача 5. Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси.
Решение:
 Домашнее задание: решить тест.
Домашнее задание: решить тест.